7.8. Matrices
A matrix is a two-dimensional array. A matrix in C can be statically allocated
as a two-dimensional array (M[n][m]), dynamically allocated with a single call
to malloc, or dynamically allocated as an array of arrays. Let’s consider
the array of arrays implementation. The first array contains n elements
(M[n]), and each element M[i] in our matrix contains an array of m
elements. The following code snippets each declare matrices of size 4 × 3:
//statically allocated matrix (allocated on stack)
int M1[4][3];
//dynamically allocated matrix (programmer friendly, allocated on heap)
int **M2, i;
M2 = malloc(4 * sizeof(int*));
for (i = 0; i < 4; i++) {
M2[i] = malloc(3 * sizeof(int));
}In the case of the dynamically allocated matrix, the main array contains a contiguous array of int pointers. Each integer
pointer points to a different array in memory. Figure 1 illustrates how we would normally visualize each of these matrices.
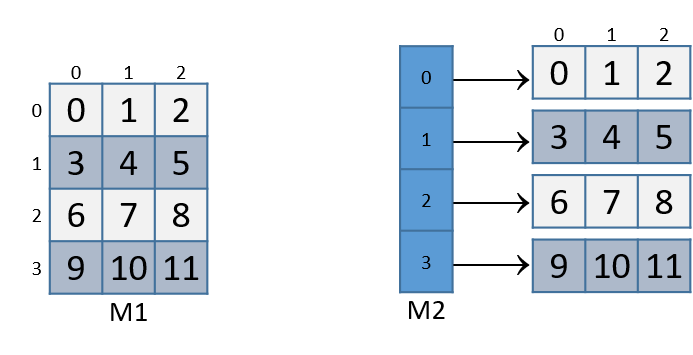
For both of these matrix declarations, element (i,j) can be accessed
using the double-indexing syntax M[i][j], where M is either M1 or M2.
However, these matrices are organized differently in memory. Even though both store
the elements in their primary array contiguously in memory, our statically
allocated matrix also stores all the rows contiguously in memory, as shown in
Figure 2.

This contiguous ordering is not guaranteed for M2.
Recall that to
contiguously allocate an n × m matrix on the heap, we should use a single
call to malloc that allocates n × m elements:
//dynamic matrix (allocated on heap, memory efficient way)
#define ROWS 4
#define COLS 3
int *M3;
M3 = malloc(ROWS * COLS * sizeof(int));Recall that with the declaration of M3, element (i,j) cannot be accessed using the M[i][j] notation. Instead,
we must index the element using the format M3[i*COLS + j].
7.8.1. Contiguous Two-Dimensional Arrays
Consider a function sumMat that takes a pointer to a contiguously allocated (either statically allocated or
memory-efficiently dynamically allocated) matrix as its first parameter, along with the numbers of rows and columns,
and returns the sum of all the elements inside the matrix.
We use scaled indexing in the code snippet that follows because it applies to both statically and dynamically allocated contiguous matrices.
Recall that the syntax m[i][j] does not work with the memory-efficient contiguous dynamic allocation previously discussed.
int sumMat(int *m, int rows, int cols) {
int i, j, total = 0;
for (i = 0; i < rows; i++){
for (j = 0; j < cols; j++){
total += m[i*cols + j];
}
}
return total;
}Here is the corresponding assembly. Each line is annotated with its English translation:
Dump of assembler code for function sumMat: 0x400686 <+0>: push %rbp # save rbp 0x400687 <+1>: mov %rsp,%rbp # update rbp (new stack frame) 0x40068a <+4>: mov %rdi,-0x18(%rbp) # copy m to %rbp-0x18 0x40068e <+8>: mov %esi,-0x1c(%rbp) # copy rows to %rbp-0x1c 0x400691 <+11>: mov %edx,-0x20(%rbp) # copy cols parameter to %rbp-0x20 0x400694 <+14>: movl $0x0,-0x4(%rbp) # copy 0 to %rbp-0x4 (total) 0x40069b <+21>: movl $0x0,-0xc(%rbp) # copy 0 to %rbp-0xc (i) 0x4006a2 <+28>: jmp 0x4006e1 <sumMat+91> # goto <sumMat+91> 0x4006a4 <+30>: movl $0x0,-0x8(%rbp) # copy 0 to %rbp-0x8 (j) 0x4006ab <+37>: jmp 0x4006d5 <sumMat+79> # goto <sumMat+79> 0x4006ad <+39>: mov -0xc(%rbp),%eax # copy i to %eax 0x4006b0 <+42>: imul -0x20(%rbp),%eax # mult i with cols, place in %eax 0x4006b4 <+46>: mov %eax,%edx # copy i*cols to %edx 0x4006b6 <+48>: mov -0x8(%rbp),%eax # copy j to %eax 0x4006b9 <+51>: add %edx,%eax # add i*cols with j, place in %eax 0x4006bb <+53>: cltq # convert %eax to a 64-bit int 0x4006bd <+55>: lea 0x0(,%rax,4),%rdx # mult (i*cols+j) by 4,put in %rdx 0x4006c5 <+63>: mov -0x18(%rbp),%rax # copy m to %rax 0x4006c9 <+67>: add %rdx,%rax # add m to (i*cols+j)*4,put in %rax 0x4006cc <+70>: mov (%rax),%eax # copy m[i*cols+j] to %eax 0x4006ce <+72>: add %eax,-0x4(%rbp) # add m[i*cols+j] to total 0x4006d1 <+75>: addl $0x1,-0x8(%rbp) # add 1 to j (j++) 0x4006d5 <+79>: mov -0x8(%rbp),%eax # copy j to %eax 0x4006d8 <+82>: cmp -0x20(%rbp),%eax # compare j with cols 0x4006db <+85>: jl 0x4006ad <sumMat+39> # if (j < cols) goto <sumMat+39> 0x4006dd <+87>: addl $0x1,-0xc(%rbp) # add 1 to i 0x4006e1 <+91>: mov -0xc(%rbp),%eax # copy i to %eax 0x4006e4 <+94>: cmp -0x1c(%rbp),%eax # compare i with rows 0x4006e7 <+97>: jl 0x4006a4 <sumMat+30> # if (i < rows) goto <sumMat+30> 0x4006e9 <+99>: mov -0x4(%rbp),%eax # copy total to %eax 0x4006ec <+102>: pop %rbp # clean up stack 0x4006ed <+103>: retq # return total
The local variables i, j, and total are loaded at addresses %rbp-0xc, %rbp-0x8,
and %rbp-0x4 on the stack, respectively. The input parameters m, row, and cols are stored at
locations %rbp-0x8, %rbp-0x1c, and %rbp-0x20, respectively. Using this knowledge, let’s zoom in on
the component that just deals with the access of element (i,j) in our matrix:
0x4006ad <+39>: mov -0xc(%rbp),%eax # copy i to %eax 0x4006b0 <+42>: imul -0x20(%rbp),%eax # multiply i with cols, place in %eax 0x4006b4 <+46>: mov %eax,%edx # copy i*cols to %edx
The first set of instructions calculates the value i*cols and places it in
register %edx. Recall that for a matrix named matrix, matrix + (i * cols)
is equivalent to &matrix[i].
0x4006b6 <+48>: mov -0x8(%rbp),%eax # copy j to %eax 0x4006b9 <+51>: add %edx,%eax # add i*cols with j, place in %eax 0x4006bb <+53>: cltq # convert %eax to a 64-bit int 0x4006bd <+55>: lea 0x0(,%rax,4),%rdx # multiply (i*cols+j) by 4,put in %rdx
The next set of instructions computes (i*cols+j)*4. The compiler multiplies
the index i*cols+j by four since each element in the matrix is a four-byte
integer, and this multiplication enables the compiler to compute the correct
offset. The cltq instruction on line <sumMat+53> is needed to sign-extend
the contents of %eax into a 64-bit integer, since that is about to be used
for address calculation.
Next, the following set of instructions adds the calculated offset to the matrix pointer and dereferences it to yield the value of element (i,j):
0x4006c5 <+63>: mov -0x18(%rbp),%rax # copy m to %rax 0x4006c9 <+67>: add %rdx,%rax # add m to (i*cols+j)*4, place in %rax 0x4006cc <+70>: mov (%rax),%eax # copy m[i*cols+j] to %eax 0x4006ce <+72>: add %eax,-0x4(%rbp) # add m[i*cols+j] to total
The first instruction loads the address of matrix m into register %rax. The
add instruction adds (i*cols + j)*4 to the address of m to correctly
calculate the offset of element (i,j). The third instruction dereferences
the address in %rax and places the value in %eax. Notice the use of %eax
as the destination component register; since our matrix contains integers, and
an integer takes up four bytes of space, component register %eax is again
used instead of %rax.
The last instruction adds the value in %eax to the accumulator total, which is located at stack address %rbp-0x4.
Let’s consider how element (1,2) is accessed in Figure 2. For convenience, the figure is reproduced below:

Element (1,2) is located at address M1 + 1*COLS + 2. Since COLS = 3,
element (1,2) corresponds to M1+5. To access the element at this location,
the compiler must multiply 5 by the size of the int data type (four bytes),
yielding the offset M1+20, which corresponds to byte x20 in the figure.
Dereferencing this location yields element 5, which is indeed element (1,2) in
the matrix.
7.8.2. Noncontiguous Matrix
The noncontiguous matrix implementation is a bit more complicated. Figure 4 visualizes how M2 may be laid out in memory.
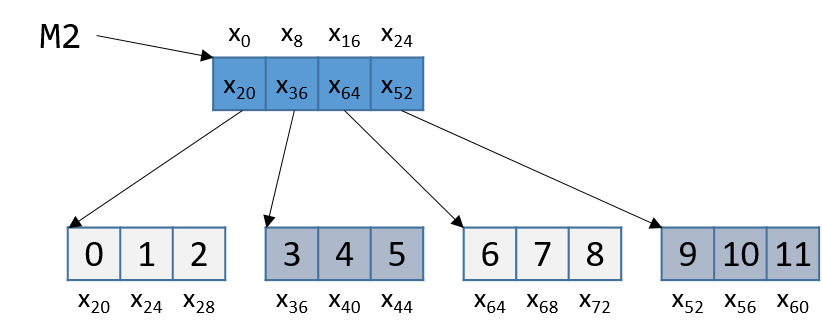
Notice that the array of pointers is contiguous, and that each array pointed to
by an element of M2 (e.g., M2[i]) is contiguous. However, the individual
arrays are not contiguous with one another. Since M2 is an array of pointers,
each element of M2 takes eight bytes of space. In contrast, as M2[i] is an
int array, each element of M2[i] is four bytes away.
The sumMatrix function in the following example takes an array of integer pointers (called matrix) as its first parameter, and
a number of rows and columns as its second and third parameters:
int sumMatrix(int **matrix, int rows, int cols) {
int i, j, total=0;
for (i = 0; i < rows; i++) {
for (j = 0; j < cols; j++) {
total += matrix[i][j];
}
}
return total;
}Even though this function looks nearly identical to the sumMat function shown earlier, the matrix
accepted by this function consists of a contiguous array of pointers. Each pointer contains the
address of a separate contiguous array, which corresponds to a separate row in the matrix.
The corresponding assembly for sumMatrix follows. Each line is annotated with its English translation.
Dump of assembler code for function sumMatrix: 0x4006ee <+0>: push %rbp # save rbp 0x4006ef <+1>: mov %rsp,%rbp # update rbp (new stack frame) 0x4006f2 <+4>: mov %rdi,-0x18(%rbp) # copy matrix to %rbp-0x18 0x4006f6 <+8>: mov %esi,-0x1c(%rbp) # copy rows to %rbp-0x1c 0x4006f9 <+11>: mov %edx,-0x20(%rbp) # copy cols to %rbp-0x20 0x4006fc <+14>: movl $0x0,-0x4(%rbp) # copy 0 to %rbp-0x4 (total) 0x400703 <+21>: movl $0x0,-0xc(%rbp) # copy 0 to %rbp-0xc (i) 0x40070a <+28>: jmp 0x40074e <sumMatrix+96> # goto <sumMatrix+96> 0x40070c <+30>: movl $0x0,-0x8(%rbp) # copy 0 to %rbp-0x8 (j) 0x400713 <+37>: jmp 0x400742 <sumMatrix+84> # goto <sumMatrix+84> 0x400715 <+39>: mov -0xc(%rbp),%eax # copy i to %eax 0x400718 <+42>: cltq # convert i to 64-bit integer 0x40071a <+44>: lea 0x0(,%rax,8),%rdx # mult i by 8, place in %rdx 0x400722 <+52>: mov -0x18(%rbp),%rax # copy matrix to %rax 0x400726 <+56>: add %rdx,%rax # put i*8 + matrix in %rax 0x400729 <+59>: mov (%rax),%rax # copy matrix[i] to %rax (ptr) 0x40072c <+62>: mov -0x8(%rbp),%edx # copy j to %edx 0x40072f <+65>: movslq %edx,%rdx # convert j to 64-bit integer 0x400732 <+68>: shl $0x2,%rdx # mult j by 4, place in %rdx 0x400736 <+72>: add %rdx,%rax # put j*4 + matrix[i] in %rax 0x400739 <+75>: mov (%rax),%eax # copy matrix[i][j] to %eax 0x40073b <+77>: add %eax,-0x4(%rbp) # add matrix[i][j] to total 0x40073e <+80>: addl $0x1,-0x8(%rbp) # add 1 to j (j++) 0x400742 <+84>: mov -0x8(%rbp),%eax # copy j to %eax 0x400745 <+87>: cmp -0x20(%rbp),%eax # compare j with cols 0x400748 <+90>: jl 0x400715 <sumMatrix+39> # if j<cols goto<sumMatrix+39> 0x40074a <+92>: addl $0x1,-0xc(%rbp) # add 1 to i (i++) 0x40074e <+96>: mov -0xc(%rbp),%eax # copy i to %eax 0x400751 <+99>: cmp -0x1c(%rbp),%eax # compare i with rows 0x400754 <+102>: jl 0x40070c <sumMatrix+30> # if i<rows goto<sumMatrix+30> 0x400756 <+104>: mov -0x4(%rbp),%eax # copy total to %eax 0x400759 <+107>: pop %rbp # restore %rbp 0x40075a <+108>: retq # return total
Once again, the variables i, j, and total are at stack addresses %rbp-0xc, %rbp-0x8,
and %rbp-0x4, respectively. The input parameters matrix, row, and cols are located at stack
addresses %rbp-0x18, %rbp-0x1c, and %rbp-0x20, respectively. Let’s zoom in on the section
that deals specifically with an access to element (i,j), or matrix[i][j]:
0x400715 <+39>: mov -0xc(%rbp),%eax # copy i to %eax 0x400718 <+42>: cltq # convert i to 64-bit integer 0x40071a <+44>: lea 0x0(,%rax,8),%rdx # multiply i by 8, place in %rdx 0x400722 <+52>: mov -0x18(%rbp),%rax # copy matrix to %rax 0x400726 <+56>: add %rdx,%rax # add i*8 to matrix, place in %rax 0x400729 <+59>: mov (%rax),%rax # copy matrix[i] to %rax (pointer)
The five instructions in this example compute matrix[i], or *(matrix+i). Since matrix[i]
contains a pointer, i is first converted to a 64-bit integer. Then, the compiler
multiplies i by eight prior to adding it to matrix to calculate the correct address offset (recall
that pointers are eight bytes in size). The instruction at <sumMatrix+59> then dereferences the calculated
address to get the element matrix[i].
Since matrix is an array of int pointers, the element located at matrix[i] is itself
an int pointer. The jth element in matrix[i] is located at offset j × 4 in the matrix[i] array.
The next set of instructions extract the jth element in array matrix[i]:
0x40072c <+62>: mov -0x8(%rbp),%edx # copy j to %edx 0x40072f <+65>: movslq %edx,%rdx # convert j to a 64-bit integer 0x400732 <+68>: shl $0x2,%rdx # multiply j by 4, place in %rdx 0x400736 <+72>: add %rdx,%rax # add j*4 to matrix[i], put in %rax 0x400739 <+75>: mov (%rax),%eax # copy matrix[i][j] to %eax 0x40073b <+77>: add %eax,-0x4(%rbp) # add matrix[i][j] to total
The first instruction in this snippet loads variable j into register %edx. The
movslq instruction at <sumMatrix+65> converts %edx into a 64-bit integer, storing
the result in 64-bit register %rdx. The compiler then uses the left shift (shl) instruction to
multiply j by four and stores the result in register %rdx. The compiler finally adds the
resulting value to the address located in matrix[i] to get the address of element matrix[i][j].
The instructions at <sumMatrix+75> and <sumMatrix+77> obtain the value at matrix[i][j] and
add the value to total.
Let’s revisit Figure 4 and consider an example access to M2[1][2]. For convenience, we reproduce the figure below:

Note that M2 starts at memory location x0. The compiler first computes the address of M2[1] by
multiplying 1 by 8 (sizeof(int *)) and adding it to the address of M2 (x0), yielding the new address
x8. A dereference of this address yields the address associated with M2[1], or x36.
The compiler then multiplies index 2 by 4 (sizeof(int)), and adds the result (8) to x36, yielding a
final address of x44. The address x44 is dereferenced, yielding the value 5.
Sure enough, the element in Figure 4 that corresponds to M2[1][2] has the value 5.