From simple stone tablets and cave paintings to written words and phonograph grooves, humans have perpetually sought to record and store information. In this chapter, we’ll characterize how the latest of humanity’s big storage breakthroughs, digital computing, represents information. We also illustrate how to interpret meaning from digital data.

Modern computers utilize a variety of media for storing information (e.g., magnetic disks, optical discs, flash memory, tapes, and simple electrical circuits). We characterize storage devices later in Chapter 11; however, for this discussion, the medium is largely irrelevant — whether there’s a laser scanning the surface of a DVD or a disk head gliding over a magnetic platter, the output from the storage device is ultimately a sequence of electrical signals. To simplify the circuitry, each signal is binary, meaning it can take only one of two states: the absence of a voltage (interpreted as zero) and the presence of a voltage (one). This chapter explores how systems encode information into binary, regardless of the original storage medium.

In binary, each signal corresponds to one bit (binary digit) of information: a zero or a one. It may be surprising that all data can be represented using just zeros and ones. Of course, as the complexity of information increases, so does the number of bits needed to represent it. Luckily, the number of unique values doubles for each additional bit in a bit sequence, so a sequence of N bits can represent 2^N unique values.

Figure 1 illustrates the growth in the number of representable values as the length of a bit sequence increases. A single bit can represent two values: 0 and 1. Two bits can represent four values: both of the one-bit values with a leading 0 (00 and 01), and both of the one-bit values with a leading 1 (10 and 11). The same pattern applies for any additional bit that extends an existing bit sequence: the new bit can be a 0 or 1, and in either case, the remaining bits represent the same range of values they did prior to the new bit being added. Thus, adding additional bits exponentially increases the number of values the new sequence can represent.

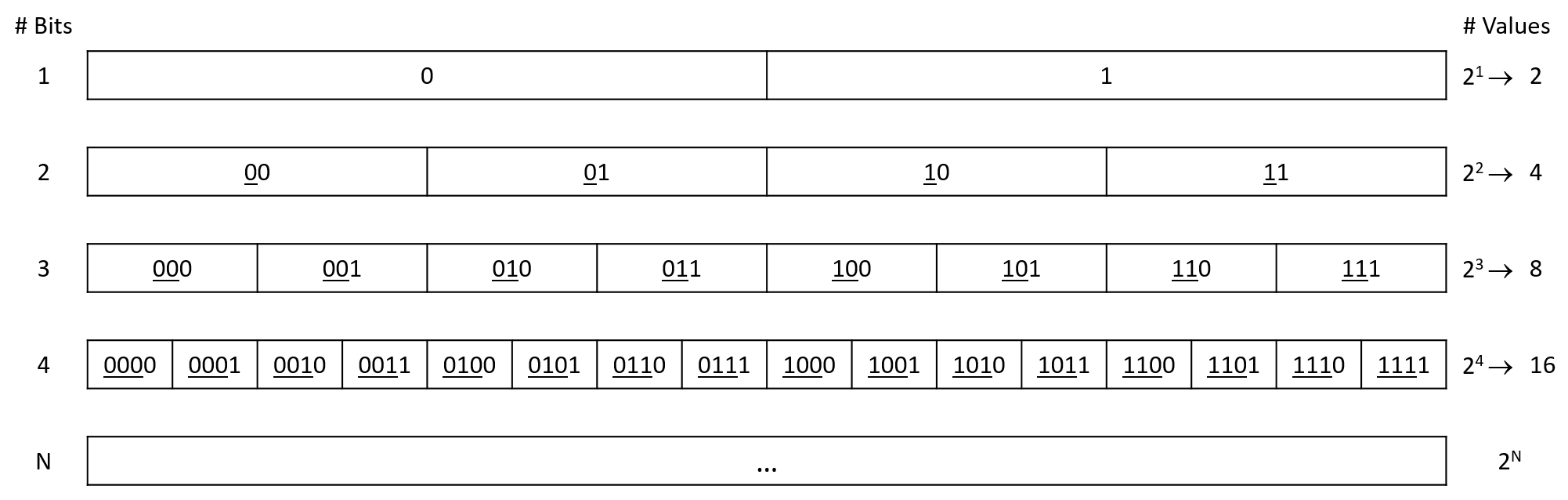
Because a single bit doesn’t represent much information, storage systems commonly group bits into longer sequences for storing more interesting values. The most ubiquitous grouping is a byte, which is a collection of eight bits. One byte represents 2⁸ = 256 unique values (0-255) — enough to enumerate the letters and common punctuation symbols of the English language. Bytes are the smallest unit of addressable memory in a computer system, meaning a program can’t ask for fewer than eight bits to store a variable.

Modern CPUs also typically define a word as either 32 bits or 64 bits, depending on the design of the hardware. The size of a word determines the "default" size a system’s hardware uses to move data from one component to another (e.g., between memory and registers). These larger sequences are necessary for storing numbers, since programs often need to count higher than 256!

If you’ve programmed in C, you know that you must declare a variable before using it. Such declarations inform the C compiler of two important properties regarding the variable’s binary representation: the number of bits to allocate for it, and the way in which the program intends to interpret those bits. Conceptually, the number of bits is straightforward, as the compiler simply looks up how many bits are associated with the declared type (e.g., a char is one byte) and associates that amount of memory with the variable. The interpretation of a sequence of bits is much more conceptually interesting. All data in a computer’s memory is stored as bits, but bits have no inherent meaning. For example, even with just a single bit, you could interpret the bit’s two values in many different ways: up and down, black and white, yes and no, on and off, etc.

Extending the length of a bit sequence expands the range of its interpretations. For example, a char variable uses the American Standard Code for Information Interchange (ASCII) encoding standard, which defines how an eight-bit binary value corresponds to English letters and punctuation symbols. Table 1 shows a small subset of the ASCII standard (for a full reference, run man ascii on the command line). There’s no special reason why the character 'X' needs to correspond to 01011000, so don’t bother memorizing the table. What matters is that every program storing letters agrees on their bit sequence interpretation, which is why ASCII is defined by a standards committee.

Any information can be encoded in binary, including rich data like graphics and audio. For example, suppose that an image encoding scheme defines 00, 01, 10, and 11 to correspond to the colors white, orange, blue, and black. Figure 2 illustrates how we might use this simple two-bit encoding strategy to draw a crude image of a fish using only 12 bytes. In part a, each cell of the image equates to one two-bit sequence. Parts b and c show the corresponding binary encoding as two-bit and byte sequences, respectively. Although this example encoding scheme is simplified for learning purposes, the general idea is similar to what real graphics systems use, albeit with many more bits for a wider range of colors.

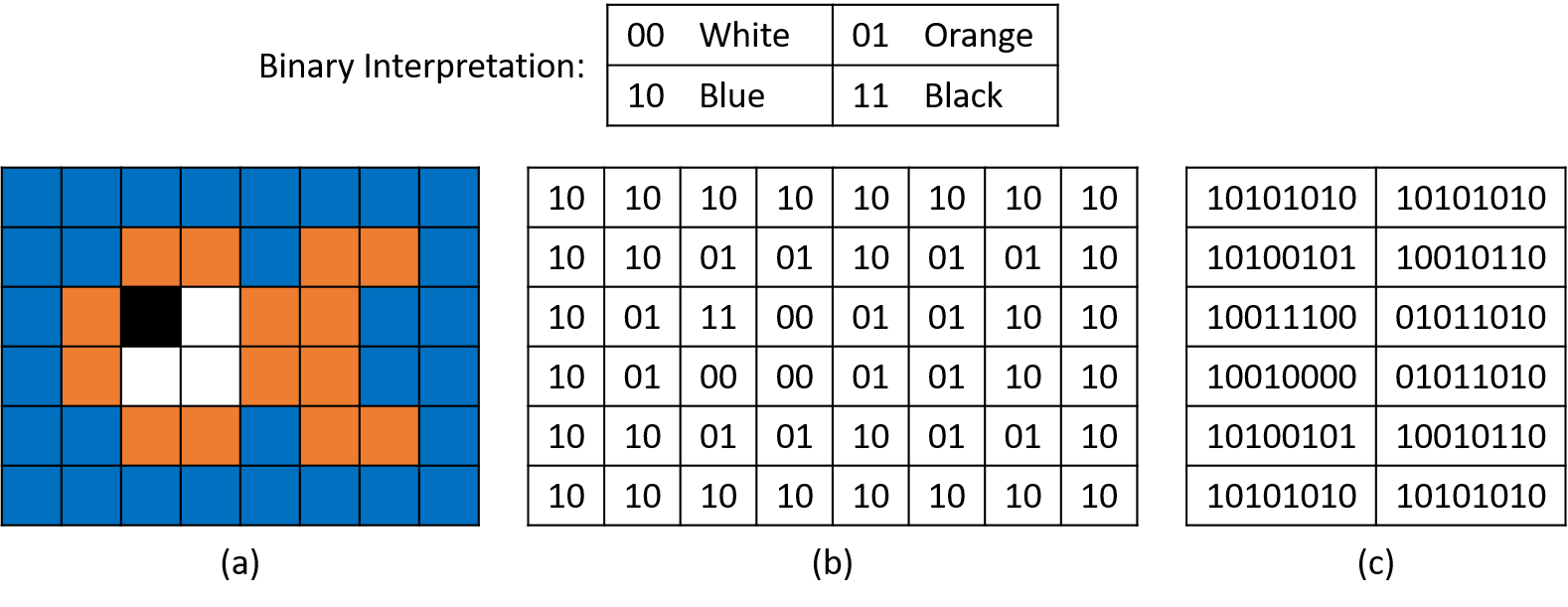
Having just introduced two encoding schemes, the same bit sequence, 01011010, might mean the character 'Z' to a text editor, whereas a graphics program might interpret it as part of a fish’s tail fin. Which interpretation is correct depends on the context. Despite the underlying bits being the same, humans often find some interpretations much easier to comprehend than others (e.g., perceiving the fish as colored cells rather than a table of bytes).

The remainder of this chapter largely deals with representing and manipulating binary numbers, but the overall point bears repeating: all information is stored in a computer’s memory as 0’s and 1’s, and it’s up to programs or the people running them to interpret the meaning of those bits.