11.3. Locality
Because memory devices vary considerably in their performance characteristics and storage capacities, modern systems integrate several forms of storage. Luckily, most programs exhibit common memory access patterns, known as locality, and designers build hardware that exploits good locality to automatically move data into an appropriate storage location. Specifically, a system improves performance by moving the subset of data that a program is actively using into storage that lives close to the CPU’s computation circuitry (for example, in a register or CPU cache). As necessary data moves up the hierarchy toward the CPU, unused data moves farther away to slower storage until the program needs it.
To a system designer, building a system that exploits locality represents an abstraction problem. The system provides an abstract view of memory devices such that it appears to programmers as if they have the sum of all memory capacities with the performance characteristics of fast on-chip storage. Of course, providing this rosy illusion to users can’t be accomplished perfectly, but by exploiting program locality, modern systems achieve good performance for most well-written programs.
Systems primarily exploit two forms of locality:
-
Temporal locality: Programs tend to access the same data repeatedly over time. That is, if a program has used a variable recently, it’s likely to use that variable again soon.
-
Spatial locality: Programs tend to access data that is nearby other, previously accessed data. "Nearby" here refers to the data’s memory address. For example, if a program accesses data at addresses N and N+4, it’s likely to access N+8 soon.
11.3.1. Locality Examples in Code
Fortunately, common programming patterns exhibit both forms of locality quite frequently. Take the following function, for example:
/* Sum up the elements in an integer array of length len. */
int sum_array(int *array, int len) {
int i;
int sum = 0;
for (i = 0; i < len; i++) {
sum += array[i];
}
return sum;
}In this code, the repetitive nature of the for loop introduces temporal
locality for i, len, sum, and array (the base address of the array), as
the program accesses each of these variables within every loop iteration.
Exploiting this temporal locality allows a system to load each variable from
main memory into the CPU cache only once. Every subsequent access can be
serviced out of the significantly faster cache.
Accesses to the array’s contents also benefit from spatial locality. Even
though the program accesses each array element only once, a modern system loads
more than one int at a time from memory to the CPU cache. That is, accessing
the first array index fills the cache with not only the first integer, but also
the next few integers after it, too. Exactly how many additional integers get
moved into the cache depends on the cache’s block size — the amount of data
transferred into the cache at once.
For example, with a 16-byte block size, a system copies four integers from memory to the cache at a time. Thus, accessing the first integer incurs the relatively high cost of accessing main memory, but the accesses to the next three are served out of cache, even if the program has never accessed them previously.
In many cases, a programmer can help a system by intentionally writing code that exhibits good locality patterns. For example, consider the nested loops that access every element of an N×N matrix (this same example appeared in this chapter’s introduction):
|
|
In both versions, the loop variables (i and j) and the accumulator variable
(total) exhibit good temporal locality because the loops repeatedly use them
in every iteration. Thus, when executing this code, a system would store those
variables in fast on-CPU storage locations to provide good performance.
However, due to the row-major order organization of a matrix in memory, the first version of the code (left) executes about five times faster than the second version (right). The disparity arises from the difference in spatial locality — the first version accesses the matrix’s values sequentially in memory (that is, in order of consecutive memory addresses). Thus, it benefits from a system that loads large blocks from memory into the cache because it pays the cost of going to memory only once for every block of values.
The second version accesses the matrix’s values by repeatedly jumping between rows across nonsequential memory addresses. It never reads from the same cache block in subsequent memory accesses, so it looks to the cache like the block isn’t needed. Thus, it pays the cost of going to memory for every matrix value it reads.
This example illustrates how a programmer can affect the system-level costs of a program’s execution. Keep these principles in mind when writing high-performance applications, particularly those that access arrays in a regular pattern.
11.3.2. From Locality to Caches
To help illustrate how the concepts of temporal and spatial locality enable cache designs, we’ll adopt an example scenario with familiar real-world objects: books. Suppose that Fiona does all of her homework at a desk in her dorm room, and the desk has a small amount of space that can store only three books. Just outside her room she keeps a bookshelf, which has much more space than the desk. Finally, across campus her college has a library with a huge variety of books. The "book storage hierarchy" in this example might look something like Figure 1. Given this scenario, we’ll explore how locality can help guide which storage location Fiona should use to store her books.
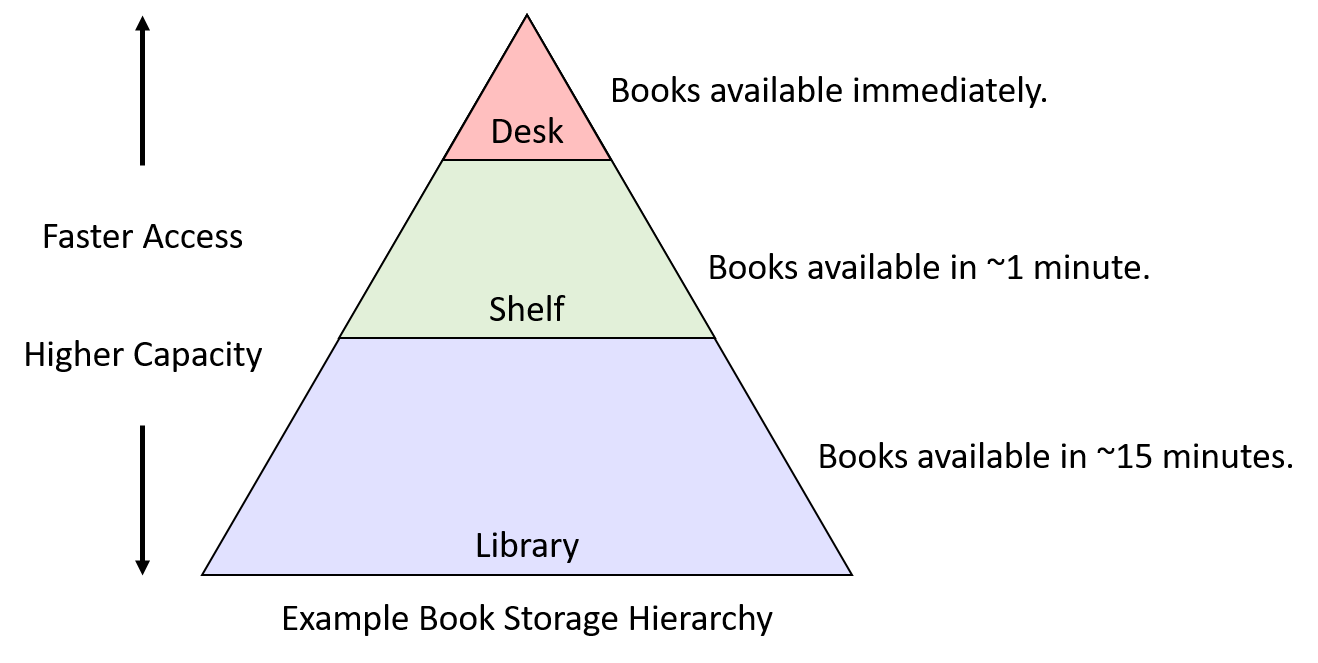
11.3.3. Temporal Locality
Temporal locality suggests that, if there’s a book Fiona uses frequently, she should keep it as close to her desk as possible. If she occasionally needs to move it to the shelf to clear up temporary work space, the cost isn’t too high, but it would be silly to take a book back to the library if she’s just going to need it again the next day. The inverse is also true: if there’s a book taking up valuable space on her desk or shelf, and she hasn’t used it for quite a while, that book seems like a good candidate for returning to the library.
So, which books should Fiona move to her precious desk space? In this example, real students would probably look at their upcoming assignments and select the books that they expect to be most useful. In other words, to make the best storage decision, they would ideally need information about future usage.
Unfortunately, hardware designers haven’t discovered how to build circuits that can predict the future. As an alternative to prediction, one could instead imagine a system that asks the programmer or user to inform the system in advance how a program will use data so that it’s placement could be optimized. Such a strategy may work well in specialized applications (for example, large databases), that exhibit very regular access patterns. However, in a general-purpose system like a personal computer, requiring advance notice from the user is too large a burden — many users would not want to (or would be unable to) provide enough detail to help the system make good decisions.
Thus, instead of relying on future access information, systems look to the past as a predictor of what will likely happen in the future. Applying this idea to the book example suggests a relatively simple (but still quite effective) strategy for governing book storage spaces:
-
When Fiona needs to use a book, she retrieves it from wherever it currently is and moves it to her desk.
-
If the desk is already full, she moves the book that she used least recently (that is, the book that has been sitting on the desk untouched for the longest amount of time) to her shelf.
-
If the shelf is full, she returns the shelf’s least recently used book to the library to free up space.
Even though this scheme may not be perfect, the simplicity makes it attractive. All it requires is the ability to move books between storage locations and a small amount of metainformation regarding the order in which books were previously used. Furthermore, this scheme captures the two initial temporal locality objectives well:
-
Frequently used books are likely to remain on the desk or shelf, preventing unnecessary trips to the library.
-
Infrequently used books eventually become the least recently used book, at which point returning them to the library makes sense.
Applying this strategy to primary storage devices looks remarkably similar to the book example: as data is loaded into CPU registers from main memory, make room for it in the CPU cache. If the cache is already full, make room in the cache by evicting the least recently used cache data to main memory. In the following caching section, we’ll explore the details of how such mechanisms are built in to modern caching systems.
11.3.4. Spatial Locality
Spatial locality suggests that, when making a trip to the library, Fiona should retrieve more than one book to reduce the likelihood of future library trips. Specifically, she should retrieve additional books that are "nearby" the one she needs, because those that are nearby seem like good candidates for books that might otherwise turn into additional library visits.
Suppose that she’s taking a literature course on the topic of Shakespeare’s histories. If in the first week of the course she’s assigned to read Henry VI, Part I, when she finds herself in the library to retrieve it, she’s likely to also find Parts II and III close by on the shelves. Even if she doesn’t yet know whether the course will assign those other two parts, it’s not unreasonable to think that she might need them. That is, the likelihood of needing them is much higher than a random book in the library, specifically because they are nearby the book she does need.
In this scenario, the likelihood increases due to the way libraries arrange
books on shelves, and programs similarly organize data in memory. For example,
a programming construct like an array or a struct stores a collection of related data
in a contiguous region of memory. When iterating over consecutive elements in
an array, there is clearly a spatial pattern in the accessed memory addresses.
Applying these spatial locality lessons to primary storage devices implies
that, when retrieving data from main memory, the system should also retrieve
the data immediately surrounding it.
In the next section, we’ll characterize cache characteristics and describe mechanisms for the hardware to make identifying and exploiting locality happen automatically.