4.3. Signed Binary Integers

So far, we’ve limited the discussion of binary numbers to unsigned (strictly non-negative) integers. This section presents an alternative interpretation of binary that incorporates negative numbers. Given that a variable has finite storage space, a signed binary encoding must distinguish between negative values, zero, and positive values. Manipulating signed numbers additionally requires a procedure for negating a number.

A signed binary encoding must divide bit sequences between negative and non-negative values. In practice, systems designers build general-purpose systems, so a 50% / 50% split is a good middle-of-the-road choice. Therefore, the signed number encodings that this chapter presents represent an equal number of negative and non-negative values.

Non-Negative versus Positive

Note that there’s a subtle but important difference between non-negative and positive. The set of strictly positive values excludes zero, whereas the non-negative set includes zero. Even after dividing the available bit sequences 50% / 50% between negative and non-negative values, one of the non-negative values must still be reserved for zero. Thus, with a fixed number of bits, a number system may end up representing more negative values than positive values (e.g., in the two’s complement system).

Signed number encodings use one bit to distinguish between the sets of negative numbers and non-negative numbers. By convention, the left-most bit indicates whether a number is negative (1) or non-negative (0). This leftmost bit is known as the high-order bit or the most significant bit.

This chapter presents two potential signed binary encodings — signed magnitude and two’s complement. Even though only one of these encodings (two’s complement) is still used in practice, comparing them will help to illustrate their important characteristics.

4.3.1. Signed Magnitude

The signed magnitude representation treats the high-order bit exclusively as a sign bit. That is, whether the high-order bit is a 0 or a 1 does not affect the absolute value of the number, it only determines whether the value is positive (high-order bit 0) or negative (high-order bit 1). Compared to two’s complement, signed magnitude makes the decimal conversion and negation procedures relatively straightforward:

  • To compute a decimal value for an N-bit signed magnitude sequence, compute the value of digits d0 through dN-2 using the familiar unsigned method. Then, check the most significant bit, dN-1: if it’s 1, the value is negative; otherwise it isn’t.

  • To negate a value, simply flip the most significant bit to change its sign.

Negation Misconception

Signed magnitude is presented purely for pedagogical purposes. Although it was used by some machines in the past (e.g., IBM’s 7090 in the 1960s), no modern systems use signed magnitude to represent integers (although a similar mechanism is part of the standard for storing floating-point values).

Unless you’re explicitly asked to consider signed magnitude, you should not assume that flipping the first bit of a binary number will negate that number’s value on a modern system.

Figure 1 shows how four-bit signed magnitude sequences correspond to decimal values. At first glance, signed magnitude might seem attractive due to its simplicity. Unfortunately, it suffers from two major drawbacks that make it unappealing. The first is that it presents two representations of zero. For example, with four bits, signed magnitude represents both zero (0b0000) and negative zero (0b1000). Consequently, it poses a challenge to hardware designers because the hardware will need to account for two possible binary sequences that are numerically equal despite having different bit values. The hardware designer’s job is much easier with just one way of representing such an important number.

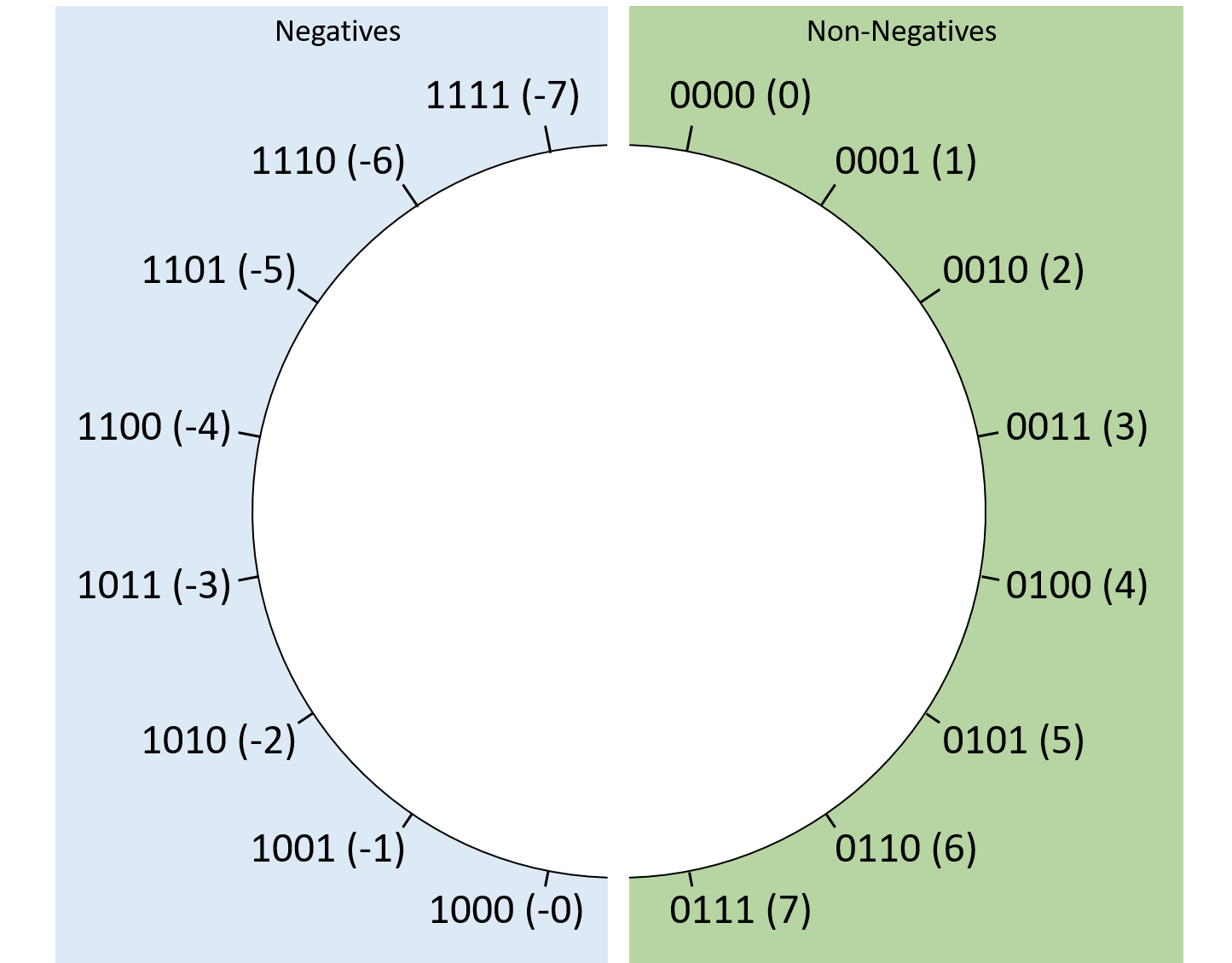
A circle with non-negative values on one side ranging from 0b0000 (0) to 0b0111 (7). The other side holds 0b1000 (-0) to 0b1111 (-7).
Figure 1. A logical layout of signed magnitude values for bit sequences of length four.

The other drawback of signed magnitude is that it exhibits an inconvenient discontinuity between negative values and zero. While we’ll cover overflow in more detail later, adding 1 to the four-bit sequence 0b1111 "rolls over" back to 0b0000. With signed magnitude, this effect means 0b1111 (-7) + 1 might be mistaken for 0 rather than the expected -6. This problem is solvable, but the solution again complicates the design of the hardware, essentially turning any transition between negative and non-negative integers into a special case that requires extra care.

For these reasons, signed magnitude has largely disappeared in practice, and two’s complement reigns supreme.

4.3.2. Two’s Complement

Two’s complement encoding solves signed magnitude’s problems in an elegant way. Like signed magnitude, the high-order bit of a two’s complement number indicates whether or not the value should be interpreted as negative. In contrast though, the high-order bit also affects the value of the number. So, how can it do both?

Computing a decimal value for an N-bit two’s complement number is similar to the familiar unsigned method, except the high-order bit’s contribution to the overall value is negated. That is, for an N-bit two’s complement sequence, instead of the first bit contributing dN-1 × 2N-1 to the sum, it contributes -dN-1 × 2N-1 (note the negative sign). Therefore, if the most significant bit is a 1, the overall value will be negative because that first bit contributes the largest absolute value to the sum. Otherwise, the first bit contributes nothing to the sum, and the result is non-negative. The full formula is:

- (dN-1 × 2N-1)    +    (dN-2 × 2N-2)    +    …​    +    (d2 × 22)    +    (d1 × 21)    +    (d0 × 20)

^ note the leading negative sign for just the first term!

Figure 2 illustrates the layout of four-bit sequences in two’s complement. This definition encodes just one representation of zero — a sequence of bits that are all 0’s. With only a single zero sequence, two’s complement represents one more negative value than positive. Using four-bit sequences as an example, two’s complement represents a minimum value of 0b1000 (-8), but a maximum value of only 0b0111 (7). Fortunately, this quirk doesn’t hinder hardware design and rarely causes problems for applications.

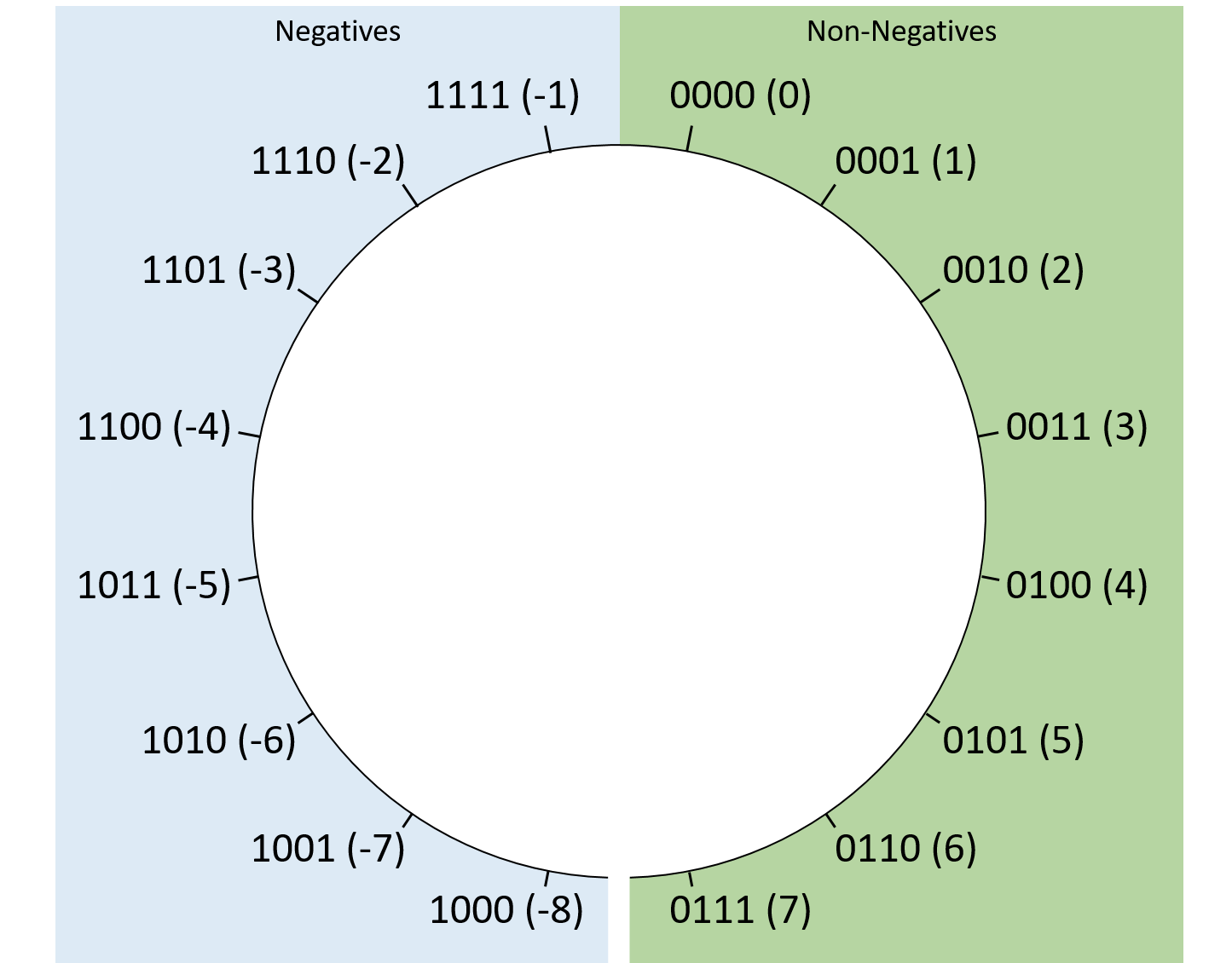
A circle with non-negative values on one side ranging from 0b0000 (0) to 0b0111 (7). The other side holds 0b1111 (-1) to 0b1000 (-8).
Figure 2. A logical layout of two’s complement values for bit sequences of length four.

Compared to signed magnitude, two’s complement also simplifies the transition between negative numbers and zero. Regardless of the number of bits used to store it, a two’s complement number consisting of all ones will always hold the value -1. Adding 1 to a bit sequence of all 1’s "rolls over" to zero, which makes two’s complement convenient, since -1 + 1 should produce zero.

Negation

Negating a two’s complement number is slightly trickier than negating a signed magnitude value. To negate an N-bit value, determine its complement with respect to 2N (this is where the encoding’s name comes from). In other words, to negate an N-bit value X, find a bit sequence Y (X's complement) such that X + Y = 2N.

Fortunately, there’s a quick shortcut for negating a two’s complement number in practice: flip all the bits and add one. For example, to negate the eight-bit value 13, first determine the binary value of 13. Because 13 is the sum of 8, 4, and 1, set the bits in positions 3, 2, and 0:

00001101  (decimal 13)

Next, "flip the bits" (change all zeros to ones, and vice versa):

11110010

Finally, adding one yields 0b11110011. Sure enough, applying the formula for interpreting a two’s complement bit sequence shows that the value is -13:

-(1 × 27)    +    (1 × 26)    +    (1 × 25)    +    (1 × 24)    +    (0 × 23)    +    (0 × 22)    +    (1 × 21)    +    (1 × 20)

  =    -128 + 64 + 32 + 16 + 0 + 0 + 2 + 1    =    -13

If you’re curious as to why this seemingly magical shortcut works, consider the eight-bit negation of 13 more formally. To find 13’s complement, solve 0b00001101 (13) + Y = 0b100000000 (28, which requires an extra bit to represent). The equation can be rearranged as Y = 0b100000000 - 0b00001101. This is clearly now a subtraction problem:

 100000000  (256)
- 00001101   (13)

While such a subtraction might seem daunting, we can express it in a way that’s easier to compute as (0b011111111 + 1) - 0b00001101. Note that this change simply expresses 28 (256) as (255 + 1). After that change, the arithmetic looks like:

 011111111  (255)  + 00000001  (1)
- 00001101   (13)

As it turns out, for any bit value b, 1 - b is equivalent to "flipping" that bit. Thus, the entire subtraction in the preceding example can be reduced to just flipping all the bits of the lower number. All that’s left is to add the remaining +1 from expressing 256 as 255 + 1. Putting it all together, we can simply flip a value’s bits and add one to compute its complement!

C Programming With Signed versus Unsigned Integers

In addition to allocating space, declaring variables in C also tells the compiler how you’d like the variable to be interpreted. When you declare an int, the compiler interprets the variable as a signed two’s complement integer. To allocate an unsigned value, declare an unsigned int.

The distinction is also relevant to C in other places, like the printf function. As this chapter has been stressing throughout, a bit sequence can be interpreted in different ways! With printf, the interpretation depends on the formatting placeholder you use. For example:

#include <stdio.h>

int main(void) {
    int example = -100;

    /* Print example int using both signed and unsigned placeholders. */
    printf("%d  %u\n", example, example);

    return 0;
}

Even though this code passes printf the same variable (example) twice, it prints -100 4294967196. Be careful to interpret your values correctly!

Sign Extension

Occasionally, you may find yourself wanting to perform an arithmetic operation on two numbers that are stored using different numbers of bits. For example, in C you may want to add a 32-bit int and a 16-bit short. In such cases, the smaller number needs to be sign extended, which is a fancy way of saying that its most significant bit gets repeated as many times as necessary to extend the length of the bit sequence to the target length. Though the compiler will take care of wrangling the bits for you in C, it’s still helpful to understand how the process works.

For example, to extend the four-bit sequence 0b0110 (6) to an eight-bit sequence, take the high-order bit (0) and prepend it four times to produce the extended value: 0b00000110 (still 6). Extending 0b1011 (-5) to an eight-bit sequence similarly takes the high-order bit (this time, 1) and prepends it four times to the resulting extended value: 0b11111011 (still -5). To verify the correctness, consider how the value changes after adding each new bit:

    0b1011 =                       -8 + 0 + 2 + 1  =  -5
   0b11011 =                  -16 + 8 + 0 + 2 + 1  =  -5
  0b111011 =             -32 + 16 + 8 + 0 + 2 + 1  =  -5
 0b1111011 =        -64 + 32 + 16 + 8 + 0 + 2 + 1  =  -5
0b11111011 =  -128 + 64 + 32 + 16 + 8 + 0 + 2 + 1  =  -5

As evidenced by the examples, numbers that are non-negative (high-order bit of zero) remain non-negative after adding zeros to the front. Likewise, negatives (high-order bit of one) remain negative after prepending ones to extended values.

Unsigned Zero Extension

For an unsigned value (e.g., a C variable explicitly declared with an unsigned qualifier), extending it to a longer bit sequence instead requires zero extension, since the unsigned qualifier prevents the value from ever being interpreted as negative. Zero extension simply prepends zeros to the high-order bits of the extended bit sequence. For example, 0b1110 (14 when interpreted as unsigned!) extends to 0b00001110 despite the original leading 1.