9.8. Matrices
A matrix is a two-dimensional (2D) array. A matrix in C can
be statically allocated as a 2D array (M[n][m]),
dynamically allocated with a single call to
malloc, or dynamically allocated as an array of arrays. Let’s consider
the array of arrays implementation. The first array contains n elements
(M[n]), and each element M[i] in our matrix contains an array of m
elements. The following code snippets each declare matrices of size 4
× 3:
//statically allocated matrix (allocated on stack)
int M1[4][3];
//dynamically allocated matrix (programmer friendly, allocated on heap)
int **M2, i;
M2 = malloc(4 * sizeof(int*));
for (i = 0; i < 4; i++) {
M2[i] = malloc(3 * sizeof(int));
}In the case of the dynamically allocated matrix, the main array contains a
contiguous array of int pointers. Each integer pointer points to a
different array in memory. Figure 1 illustrates how we would
normally visualize each of these matrices.
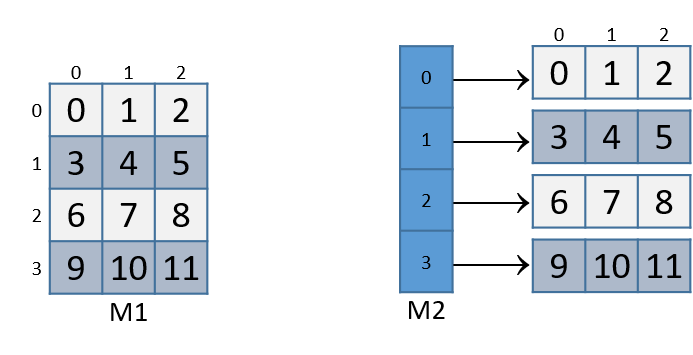
For both of the these matrix declarations, element (i,j) can be accessed
using the double-indexing syntax M[i][j], where M is either M1 or
M2. However, these matrices are organized differently in memory.
Even though both store the elements in their primary array contiguously in memory,
our statically allocated matrix also stores all the rows contiguously in
memory:

This contiguous ordering is not guaranteed for M2.
Recall that to
contiguously allocate an n × m matrix on the heap, we should use a
single call to malloc that allocates n × m elements:
//dynamic matrix (allocated on heap, memory efficient way)
#define ROWS 4
#define COLS 3
int *M3;
M3 = malloc(ROWS*COLS*sizeof(int));Recall that with the declaration of M3, element (i,j) cannot be
accessed using the M[i][j] notation. Instead, we must index the element
using the format: M3[i*cols + j].
9.8.1. Contiguous Two-Dimensional Arrays
Consider a function sumMat that takes a pointer to a contiguously
allocated (either statically allocated or memory-efficient dynamically
allocated) matrix as its first parameter, along with a number of rows and
columns, and returns the sum of all the elements inside the matrix.
We use scaled indexing in the code snippet that follows because it applies to both
statically and dynamically allocated contiguous matrices. Recall that the
syntax m[i][j] does not work with the memory-efficient contiguous dynamic
allocation previously discussed.
int sumMat(int *m, int rows, int cols) {
int i, j, total = 0;
for (i = 0; i < rows; i++){
for (j = 0; j < cols; j++){
total += m[i*cols + j];
}
}
return total;
}Here is the corresponding assembly. Each line is annotated with its English translation:
Dump of assembler code for function sumMat: 0x884 <+0>: sub sp, sp, #0x20 // grow stack by 32 bytes (new frame) 0x888 <+4>: str x0, [sp, #8] // store m in location sp + 8 0x88c <+8>: str w1, [sp, #4] // store rows in location sp + 4 0x890 <+12>: str w2, [sp] // store cols at top of stack 0x894 <+16>: str wzr, [sp, #28] // store zero at sp + 28 (total) 0x898 <+20>: str wzr, [sp, #20] // store zero at sp + 20 (i) 0x89c <+24>: b 0x904 <sumMat+128> // goto <sumMat+128> 0x8a0 <+28>: str wzr, [sp, #24] // store zero at sp + 24 (j) 0x8a4 <+32>: b 0x8e8 <sumMat+100> // goto <sumMat+100> 0x8a8 <+36>: ldr w1, [sp, #20] // w1 = i 0x8ac <+40>: ldr w0, [sp] // w0 = cols 0x8b0 <+44>: mul w1, w1, w0 // w1 = cols * i 0x8b4 <+48>: ldr w0, [sp, #24] // w0 = j 0x8b8 <+52>: add w0, w1, w0 // w0 = (cols * i) + j 0x8bc <+56>: sxtw x0, w0 // x0 = signExtend(cols * i + j) 0x8c0 <+60>: lsl x0, x0, #2 // x0 = (cols * i + j) * 4 0x8c4 <+64>: ldr x1, [sp, #8] // x1 = m 0x8c8 <+68>: add x0, x1, x0 // x0 = m+(cols*i+j)*4 (or &m[i*cols+j]) 0x8cc <+72>: ldr w0, [x0] // w0 = m[i*cols + j] 0x8d0 <+76>: ldr w1, [sp, #28] // w1 = total 0x8d4 <+80>: add w0, w1, w0 // w0 = total + m[i*cols + j] 0x8d8 <+84>: str w0, [sp, #28] // total is now (total + m[i*cols + j]) 0x8dc <+88>: ldr w0, [sp, #24] // w0 = j 0x8e0 <+92>: add w0, w0, #0x1 // w0 = j + 1 0x8e4 <+96>: str w0, [sp, #24] // update j with (j + 1) 0x8e8 <+100>: ldr w1, [sp, #24] // w1 = j 0x8ec <+104>: ldr w0, [sp] // w0 = cols 0x8f0 <+108>: cmp w1, w0 // compare j with cols 0x8f4 <+112>: b.lt 0x8a8 <sumMat+36> // if (j < cols) goto <sumMat+36> 0x8f8 <+116>: ldr w0, [sp, #20] // w0 = i 0x8fc <+120>: add w0, w0, #0x1 // w0 = i + 1 0x900 <+124>: str w0, [sp, #20] // update i with (i+1) 0x904 <+128>: ldr w1, [sp, #20] // w1 = i 0x908 <+132>: ldr w0, [sp, #4] // w0 = rows 0x90c <+136>: cmp w1, w0 // compare i with rows 0x910 <+140>: b.lt 0x8a0 <sumMat+28> // if (i < rows) goto <sumMat+28> 0x914 <+144>: ldr w0, [sp, #28] // w0 = total 0x918 <+148>: add sp, sp, #0x20 // revert stack to prior state 0x91c <+152>: ret // return (total)
The local variables i, j, and total are stored at stack locations sp
+ 20, sp + 24 and sp + 28, respectively. The input parameters m, row,
and cols are stored at locations sp + 8, sp + 4, and sp (top of
stack), respectively. Using this knowledge, let’s zoom in on the component
that just deals with the access of element (i,j) in our matrix (0x8a8
to 0x8d8):
0x8a8 <+36>: ldr w1, [sp, #20] // w1 = i 0x8ac <+40>: ldr w0, [sp] // w0 = cols 0x8b0 <+44>: mul w1, w1, w0 // w1 = cols * i
The first set of instructions calculates the value cols * i and
places it in register w1. Recall that for some matrix called matrix,
matrix+i*cols is equivalent to &matrix[i].
0x8b4 <+48>: ldr w0, [sp, #24] // w0 = j 0x8b8 <+52>: add w0, w1, w0 // w0 = (cols * i) + j 0x8bc <+56>: sxtw x0, w0 // x0 = signExtend(cols * i + j) 0x8c0 <+60>: lsl x0, x0, #2 // x0 = (cols * i + j) * 4
The next set of instructions computes (cols*i + j) * 4. The compiler
multiplies the index cols * i + j by four because each element in the matrix
is a four-byte integer, and this multiplication enables the compiler to
compute the correct offset. The sxtw instruction on line <sumMat+56>
sign-extends the contents of w0 into a 64-bit integer, since that value is
needed for address calculation.
The following set of instructions adds the calculated offset to the matrix pointer and dereferences it to yield the value of element (i,j):
0x8c4 <+64>: ldr x1, [sp, #8] // x1 = m 0x8c8 <+68>: add x0, x1, x0 // x0 = m + (cols*i + j)*4 (or &m[i*cols + j]) 0x8cc <+72>: ldr w0, [x0] // w0 = m[i*cols + j] 0x8d0 <+76>: ldr w1, [sp, #28] // w1 = total 0x8d4 <+80>: add w0, w1, w0 // w0 = total + m[i*cols + j] 0x8d8 <+84>: str w0, [sp, #28] // update total with (total + m[i*cols + j])
The first instruction loads the address of matrix m into register x1.
The add instruction adds (cols * i + j) * 4 to the address of m to
correctly calculate the offset of element (i,j) and then places the result in
register x0. The third instruction dereferences the address in x0 and
places the value (m[i * cols + j]) into w0. Notice the use of w0 as the
destination component register; since our matrix contains integers, and
integers take up four bytes of space, component register w0 is again used
instead of x0.
The last three instructions load the current value of total into register
w1, add total with m[i * cols + j], and then update total with the
resulting sum.
Let’s consider how element (1,2) is accessed in matrix M1 (figure reproduced below).

Element (1,2) is located at address
M1 + 1 * cols + 2. Since cols = 3, element (1,2) corresponds to M1 + 5.
To access the element at this location, the compiler must multiply 5 by
the size of the int data type (four bytes), yielding the offset M1 + 20,
which corresponds to byte a20 in the figure. Dereferencing this location
yields element 5, which is indeed element (1,2) in the matrix.
9.8.2. Noncontiguous Matrix
The noncontiguous matrix implementation is a bit more complicated.
Figure 4 visualizes how M2 may be laid out in memory.
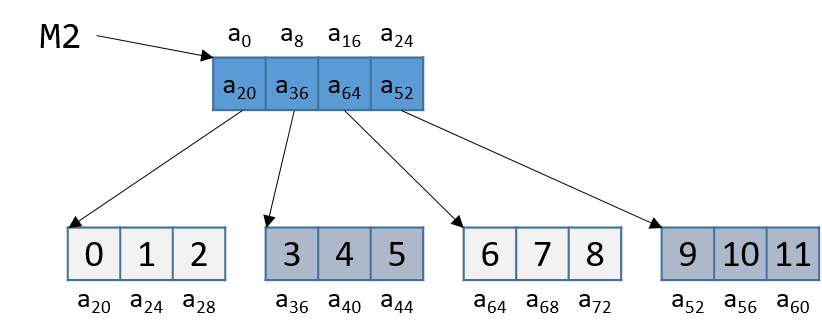
Notice that the array of pointers in M2 is contiguous, and that each array
pointed to by some element of M2 (e.g., M2[i]) is contiguous. However,
the individual arrays are not contiguous with one another. Since M2 is an
array of pointers, each element of M2 takes eight bytes of space. In
contrast, because each M2[i] is an int array, the elements of every
M2[i] array are four bytes apart.
The sumMatrix function in the follow example takes an array of integer pointers (called
matrix) as its first parameter, and a number of rows and columns as its
second and third parameters:
int sumMatrix(int **matrix, int rows, int cols) {
int i, j, total=0;
for (i = 0; i < rows; i++) {
for (j = 0; j < cols; j++) {
total += matrix[i][j];
}
}
return total;
}Even though this function looks nearly identical to the sumMat function shown
earlier, the matrix accepted by this function consists of a contiguous array
of pointers. Each pointer contains the address of a separate contiguous
array, which corresponds to a separate row in the matrix.
The corresponding assembly for sumMatrix follows. Each line is annotated
with its English translation.
Dump of assembler code for function sumMatrix: 0x920 <+0>: sub sp, sp, #0x20 // grow stack 32 bytes (new frame) 0x924 <+4>: str x0, [sp, #8] // store matrix at sp + 8 0x928 <+8>: str w1, [sp, #4] // store rows at sp + 4 0x92c <+12>: str w2, [sp] // store cols at sp (top of stack) 0x930 <+16>: str wzr, [sp, #28] // store 0 at sp + 28 (total) 0x934 <+20>: str wzr, [sp, #20] // store 0 at sp + 20 (i) 0x938 <+24>: b 0x99c <sumMatrix+124> // goto <sumMatrix+124> 0x93c <+28>: str wzr, [sp, #24] // store 0 at sp + 24 (j) 0x940 <+32>: b 0x980 <sumMatrix+96> // goto <sumMatrix+96> 0x944 <+36>: ldrsw x0, [sp, #20] // x0 = signExtend(i) 0x948 <+40>: lsl x0, x0, #3 // x0 = i << 3 (or i * 8) 0x94c <+44>: ldr x1, [sp, #8] // x1 = matrix 0x950 <+48>: add x0, x1, x0 // x0 = matrix + i * 8 0x954 <+52>: ldr x1, [x0] // x1 = matrix[i] 0x958 <+56>: ldrsw x0, [sp, #24] // x0 = signExtend(j) 0x95c <+60>: lsl x0, x0, #2 // x0 = j << 2 (or j * 4) 0x960 <+64>: add x0, x1, x0 // x0 = matrix[i] + j * 4 0x964 <+68>: ldr w0, [x0] // w0 = matrix[i][j] 0x968 <+72>: ldr w1, [sp, #28] // w1 = total 0x96c <+76>: add w0, w1, w0 // w0 = total + matrix[i][j] 0x970 <+80>: str w0, [sp, #28] // store total = total+matrix[i][j] 0x974 <+84>: ldr w0, [sp, #24] // w0 = j 0x978 <+88>: add w0, w0, #0x1 // w0 = j + 1 0x97c <+92>: str w0, [sp, #24] // update j with (j + 1) 0x980 <+96>: ldr w1, [sp, #24] // w1 = j 0x984 <+100>: ldr w0, [sp] // w0 = cols 0x988 <+104>: cmp w1, w0 // compare j with cols 0x98c <+108>: b.lt 0x944 <sumMatrix+36> // if (j < cols) goto <sumMatrix+36> 0x990 <+112>: ldr w0, [sp, #20] // w0 = i 0x994 <+116>: add w0, w0, #0x1 // w0 = i + 1 0x998 <+120>: str w0, [sp, #20] // update i with (i + 1) 0x99c <+124>: ldr w1, [sp, #20] // w1 = i 0x9a0 <+128>: ldr w0, [sp, #4] // w0 = rows 0x9a4 <+132>: cmp w1, w0 // compare i with rows 0x9a8 <+136>: b.lt 0x93c <sumMatrix+28> // if (i < rows) goto <sumMatrix+28> 0x9ac <+140>: ldr w0, [sp, #28] // w0 = total 0x9b0 <+144>: add sp, sp, #0x20 // revert stack to its original form 0x9b4 <+148>: ret // return (total)
Again, variables i, j, and total are at stack addresses sp,
20sp + 24, and sp + 28, respectively. The input parameters matrix,
row, and cols are located at stack addresses sp + 8, sp + 4, and
sp (top of stack), respectively. Let’s zoom in on the section that deals
specifically with an access to element (i, j), or matrix[i][j], which
is between instructions 0x944 and 0x970:
0x944 <+36>: ldrsw x0, [sp, #20] // x0 = signExtend(i) 0x948 <+40>: lsl x0, x0, #3 // x0 = i << 3 (or i * 8) 0x94c <+44>: ldr x1, [sp, #8] // x1 = matrix 0x950 <+48>: add x0, x1, x0 // x0 = matrix + i * 8 0x954 <+52>: ldr x1, [x0] // x1 = matrix[i]
The five instructions in this example compute matrix[i], or *(matrix+i). Since
matrix[i] contains a pointer, i is first converted to a 64-bit integer.
Then, the compiler multiplies i by eight by using a shift operation, and then
adds the result to matrix to yield the correct address offset (recall that
pointers are eight bytes in size). The instruction at <sumMatrix+52> then
dereferences the calculated address to get the element matrix[i].
Since matrix is an array of int pointers, the element located at
matrix[i] is itself an int pointer. The jth element in matrix[i]
is located at offset j × 4 in the matrix[i] array.
The next set of instructions extract the jth element in
array matrix[i]:
0x958 <+56>: ldrsw x0, [sp, #24] // x0 = signExtend(j) 0x95c <+60>: lsl x0, x0, #2 // x0 = j << 2 (or j * 4) 0x960 <+64>: add x0, x1, x0 // x0 = matrix[i] + j * 4 0x964 <+68>: ldr w0, [x0] // w0 = matrix[i][j] 0x968 <+72>: ldr w1, [sp, #28] // w1 = total 0x96c <+76>: add w0, w1, w0 // w0 = total + matrix[i][j] 0x970 <+80>: str w0, [sp, #28] // store total = total + matrix[i][j]
The first instruction in this snippet loads variable j into register x0,
sign-extending it in the process. The compiler then uses the left shift
(lsl) instruction to multiply j by four and stores the result in register
x0. The compiler finally adds the resulting value to the address located
in matrix[i] to get the address of element matrix[i][j], or
&matrix[i][j]. The instruction at <sumMatrix+68> then dereferences the
address to get the value at matrix[i][j], which is then stored in
register w0. Lastly, the instructions from <sumMatrix+72> through
<sumMatrix+80> add total to matrix[i][j] and update the variable
total with the resulting sum.
Let’s consider an example access to M2[1][2] (figure reproduced below).

Note that M2 starts at memory location a0. The compiler first computes the
address of M2[1] by multiplying 1 by 8 (sizeof(int *)) and adding it to the
address of M2 (a0), yielding the new address a8. A dereference of this
address yields the address associated with M2[1], or a36. The compiler
then multiplies index 2 by 4 (sizeof(int)), and adds the result (8) to a36,
yielding a final address of a44. The address a44 is dereferenced, yielding
the value 5. Sure enough, the element in [DynamicMatrix6a64repro] that
corresponds to M2[1][2] has the value 5.