15.2. Distributed Memory Systems, Message Passing, and MPI
Chapter 14 describes mechanisms like Pthreads and OpenMP that programs use to take advantage of multiple CPU cores on a shared memory system. In such systems, each core shares the same physical memory hardware, allowing them to communicate data and synchronize their behavior by reading from and writing to shared memory addresses. Although shared memory systems make communication relatively easy, their scalability is limited by the number of CPU cores in the system.
As of 2019, high-end commercial server CPUs generally provide a maximum of 64 cores. For some tasks, though, even a few hundred CPU cores isn’t close enough. For example, imagine trying to simulate the fluid dynamics of the Earth’s oceans or index the entire contents of the World Wide Web to build a search application. Such massive tasks require more physical memory and processors than any single computer can provide. Thus, applications that require a large number of CPU cores run on systems that forego shared memory. Instead, they execute on systems built from multiple computers, each with their own CPU(s) and memory, that communicate over a network to coordinate their behavior.
A collection of computers working together is known as a distributed memory system (or often just distributed system).
|
A Note on Chronology
Despite the order in which they’re presented in this book, systems designers built distributed systems long before mechanisms like threads or OpenMP existed. |
Some distributed memory systems integrate hardware more closely than others. For example, a supercomputer is a high-performance system in which many compute nodes are tightly coupled (closely integrated) to a fast interconnection network. Each compute node contains its own CPU(s), GPU(s), and memory, but multiple nodes might share auxiliary resources like secondary storage and power supplies. The exact level of hardware sharing varies from one supercomputer to another.
On the other end of the spectrum, a distributed application might run on a loosely coupled (less integrated) collection of fully autonomous computers (nodes) connected by a traditional local area network (LAN) technology like Ethernet. Such a collection of nodes is known as a commodity off-the-shelf (COTS) cluster. COTS clusters typically employ a shared-nothing architecture in which each node contains its own set of computation hardware (CPU(s), GPU(s), memory, and storage). Figure 1 illustrates a shared-nothing distributed system consisting of two shared-memory computers.
15.2.1. Parallel and Distributed Processing Models
Application designers often organize distributed applications using tried-and-true designs. Adopting application models like these helps developers reason about an application because its behavior will conform to well-understood norms. Each model has its unique benefits and drawbacks — there’s no one-size-fits-all solution. We briefly characterize a few of the more common models below, but note that we’re not presenting an exhaustive list.
Client/Server
The client/server model is an extremely common application model that divides an application’s responsibilities among two actors: client processes and server processes. A server process provides a service to clients that ask for something to be done. Server processes typically wait at well-known addresses to receive incoming connections from clients. Upon making a connection, a client sends requests to the server process, which either satisfies those requests (e.g., by fetching a requested file) or reports an error (e.g., the file not existing or the client can’t be properly authenticated).
Although you may not have considered it, you accessed the textbook you’re
reading right now via the client/server model! Your web browser (client)
connected to a website (server) at a public address (diveintosystems.org) to
retrieve the book’s contents.
Pipeline
The pipeline model divides an application into a distinct sequence of steps, each of which can process data independently. This model works well for applications whose workflow involves linear, repetitive tasks over large data inputs. For example, consider the production of computer-animated films. Each frame of the film must be processed through a sequence of steps that transform the frame (e.g., adding textures or applying lighting). Because each step happens independently in a sequence, animators can speed up rendering by processing frames in parallel across a large cluster of computers.
Boss/Worker
In the boss/worker model, one process acts as a central coordinator and distributes work among the processes at other nodes. This model works well for problems that require processing a large, divisible input. The boss divides the input into smaller pieces and assigns one or more pieces to each worker. In some applications, the boss might statically assign each worker exactly one piece of the input. In other cases, the workers might repeatedly finish a piece of the input and then return to the boss to dynamically retrieve the next input chunk. Later in this section, we’ll present an example program in which a boss divides an array among many workers to perform scalar multiplication on an array.
Note that this model is sometimes called other names, like "master/worker" or other variants, but the main idea is the same.
Peer-to-Peer
Unlike the boss/worker model, a peer-to-peer application avoids relying on a centralized control process. Instead, peer processes self-organize the application into a structure in which they each take on roughly the same responsibilities. For example, in the BitTorrent file sharing protocol, each peer repeatedly exchanges parts of a file with others until they’ve all received the entire file.
Lacking a centralized component, peer-to-peer applications are generally robust to node failures. On the other hand, peer-to-peer applications typically require complex coordination algorithms, making them difficult to build and rigorously test.
15.2.2. Communication Protocols
Whether they are part of a supercomputer or a COTS cluster, processes in a distributed memory system communicate via message passing, whereby one process explicitly sends a message to processes on one or more other nodes, which receive it. It’s up to the applications running on the system to determine how to utilize the network — some applications require frequent communication to tightly coordinate the behavior of processes across many nodes, whereas other applications communicate to divide up a large input among processes and then mostly work independently.
A distributed application formalizes its communication expectations by defining a communication protocol, which describes a set of rules that govern its use of the network, including:
-
When a process should send a message
-
To which process(es) it should send the message
-
How to format the message
Without a protocol, an application might fail to interpret messages properly or even deadlock. For example, if an application consists of two processes, and each process waits for the other to send it a message, neither process will ever make progress. Protocols add structure to communication to reduce the likelihood of such failures.
To implement a communication protocol, applications require basic functionality for tasks like sending and receiving messages, naming processes (addressing), and synchronizing process execution. Many applications look to the Message Passing Interface for such functionality.
15.2.3. Message Passing Interface (MPI)
The Message Passing Interface (MPI) defines (but does not itself implement) a standardized interface that applications can use to communicate in a distributed memory system. By adopting the MPI communication standard, applications become portable, meaning that they can be compiled and executed on many different systems. In other words, as long as an MPI implementation is installed, a portable application can move from one system to another and expect to execute properly, even if the systems have different underlying characteristics.
MPI allows a programmer to divide an application into multiple processes. It
assigns each of an application’s processes a unique identifier, known as a
rank, which ranges from 0 to N-1 for an application with N processes. A
process can learn its rank by calling the MPI_Comm_rank function, and it
can learn how many processes are executing in the application by calling
MPI_Comm_size. To send a message, a process calls MPI_Send and
specifies the rank of the intended recipient. Similarly, a process calls
MPI_Recv to receive a message, and it specifies whether to wait for a
message from a specific node or to receive a message from any sender (using the
constant MPI_ANY_SOURCE as the rank).
In addition to the basic send and receive functions, MPI also defines a variety
of functions that make it easier for one process to communicate data to
multiple recipients. For example, MPI_Bcast allows one process to send a
message to every other process in the application with just one function call.
It also defines a pair of functions, MPI_Scatter and MPI_Gather, that
allow one process to divide up an array and distribute the pieces among
processes (scatter), operate on the data, and then later retrieve all the
data to coalesce the results (gather).
Because MPI specifies only a set of functions and how they should behave,
each system designer can implement MPI’s functionality in a way that matches
the capabilities of their particular system. For example, a system with an
interconnect network that supports broadcasting (sending one copy of a message
to multiple recipients at the same time) might be able to implement MPI’s
MPI_Bcast function more efficiently than a system without such support.
15.2.4. MPI Hello World
As an introduction to MPI programming, consider the "hello world" program (hello_world_mpi.c) presented here:
#include <stdio.h>
#include <unistd.h>
#include "mpi.h"
int main(int argc, char **argv) {
int rank, process_count;
char hostname[1024];
/* Initialize MPI. */
MPI_Init(&argc, &argv);
/* Determine how many processes there are and which one this is. */
MPI_Comm_size(MPI_COMM_WORLD, &process_count);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
/* Determine the name of the machine this process is running on. */
gethostname(hostname, 1024);
/* Print a message, identifying the process and machine it comes from. */
printf("Hello from %s process %d of %d\n", hostname, rank, process_count);
/* Clean up. */
MPI_Finalize();
return 0;
}When starting this program, MPI simultaneously executes multiple copies of it
as independent processes across one or more computers. Each process makes
calls to MPI to determine how many total processes are executing (with
MPI_Comm_size) and which process it is among those processes (the process’s
rank, with MPI_Comm_rank). After looking up this information, each process
prints a short message containing the rank and name of the computer
(hostname) it’s running on before terminating.
|
Running MPI Code
|
To compile this example, invoke the mpicc compiler program, which executes an
MPI-aware version of gcc to build the program and link it against MPI
libraries:
$ mpicc -o hello_world_mpi hello_world_mpi.c
To execute the program, use the mpirun utility to start up several parallel
processes with MPI. The mpirun command needs to be told which computers to run processes
on (--hostfile) and how many processes to run at each machine (-np). Here,
we provide it with a file named hosts.txt that tells mpirun to create four
processes across two computers, one named lemon, and another named orange:
$ mpirun -np 8 --hostfile hosts.txt ./hello_world_mpi Hello from lemon process 4 of 8 Hello from lemon process 5 of 8 Hello from orange process 2 of 8 Hello from lemon process 6 of 8 Hello from orange process 0 of 8 Hello from lemon process 7 of 8 Hello from orange process 3 of 8 Hello from orange process 1 of 8
|
MPI Execution Order
You should never make any assumptions about the order in which MPI processes will execute. The processes start up on multiple machines, each of which has its own OS and process scheduler. If the correctness of your program requires that processes run in a particular order, you must ensure that the proper order occurs — for example, by forcing certain processes to pause until they receive a message. |
15.2.5. MPI Scalar Multiplication
For a more substantive MPI example, consider performing scalar multiplication on an array. This example adopts the boss/worker model — one process divides the array into smaller pieces and distributes them among worker processes. Note that in this implementation of scalar multiplication, the boss process also behaves as a worker and multiplies part of the array after distributing sections to the other workers.
To benefit from working in parallel, each process multiplies just its local piece of the array by the scalar value, and then the workers all send the results back to the boss process to form the final result. At several points in the program, the code checks to see whether the rank of the process is zero:
if (rank == 0) {
/* This code only executes at the boss. */
}This check ensures that only one process (the one with rank 0) plays the role of the boss. By convention, MPI applications often choose rank 0 to perform one-time tasks because no matter how many processes there are, one will always be given rank 0 (even if just a single process is executing).
MPI Communication
The boss process begins by determining the scalar value and initial input array. In a real scientific computing application, the boss would likely read such values from an input file. To simplify this example, the boss uses a constant scalar value (10) and generates a simple 40-element array (containing the sequence 0 to 39) for illustrative purposes.
This program requires communication between MPI processes for three important tasks:
-
The boss sends the scalar value and the size of the array to all of the workers.
-
The boss divides the initial array into pieces and sends a piece to each worker.
-
Each worker multiplies the values in its piece of the array by the scalar and then sends the updated values back to the boss.
Broadcasting Important Values
To send the scalar value to the workers, the example program uses the
MPI_Bcast function, which allows one MPI process to send the same value to
all the other MPI processes with one function call:
/* Boss sends the scalar value to every process with a broadcast. */
MPI_Bcast(&scalar, 1, MPI_INT, 0, MPI_COMM_WORLD);This call sends one integer (MPI_INT) starting from the address of the
scalar variable from the process with rank 0 to every other process
(MPI_COMM_WORLD). All the worker processes (those with nonzero rank)
receive the broadcast into their local copy of the scalar variable, so when
this call completes, every process knows the scalar value to use.
|
MPI_Bcast Behavior
Every process executes |
Similarly, the boss broadcasts the total size of the array to every other
process. After learning the total array size, each process sets a local_size
variable by dividing the total array size by the number of MPI processes. The
local_size variable represents how many elements each worker’s piece of the
array will contain. For example, if the input array contains 40 elements and
the application consists of eight processes, each process is responsible for a
five-element piece of the array (40 / 8 = 5). To keep the example simple, it
assumes that the number of processes evenly divides the size of the array:
/* Each process determines how many processes there are. */
MPI_Comm_size(MPI_COMM_WORLD, &process_count);
/* Boss sends the total array size to every process with a broadcast. */
MPI_Bcast(&array_size, 1, MPI_INT, 0, MPI_COMM_WORLD);
/* Determine how many array elements each process will get.
* Assumes the array is evenly divisible by the number of processes. */
local_size = array_size / process_count;Distributing the Array
Now that each process knows the scalar value and how many values it’s responsible for multiplying, the boss must divide the array into pieces and distribute them among the workers. Note that in this implementation, the boss (rank 0) also participates as a worker. For example, with a 40-element array and eight processes (ranks 0-7), the boss should keep array elements 0-4 for itself (rank 0), send elements 5-9 to rank 1, elements 10-14 to rank 2, and so on. Figure 2 shows how the boss assigns pieces of the array to each MPI process.
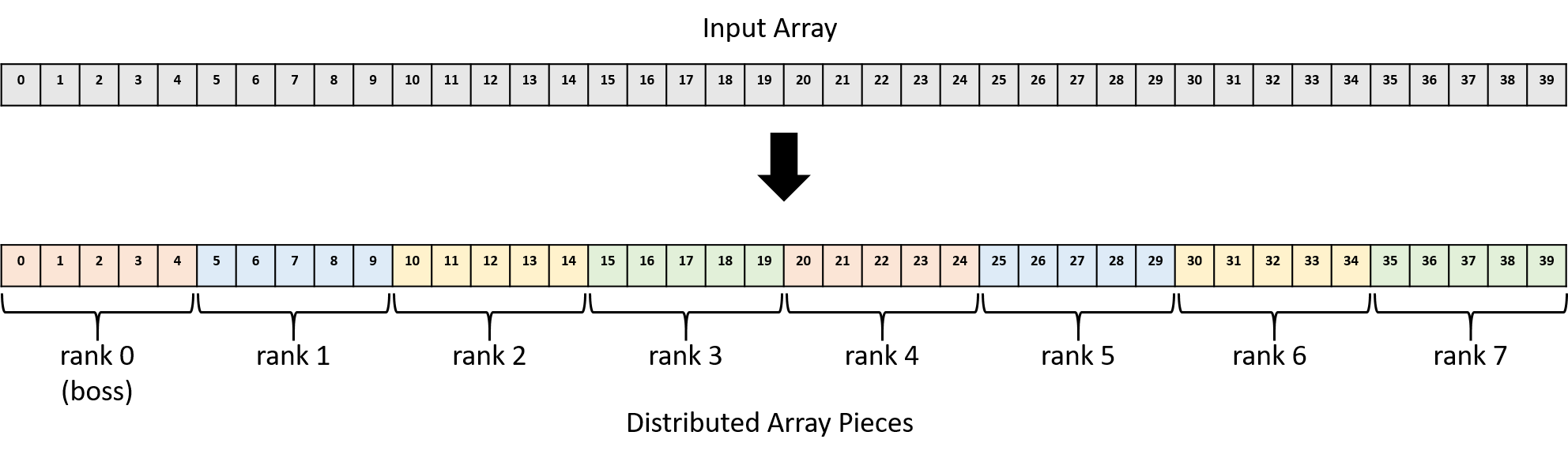
One option for distributing pieces of the array to each worker combines
MPI_Send calls at the boss with an MPI_Recv call at each worker:
if (rank == 0) {
int i;
/* For each worker process, send a unique chunk of the array. */
for (i = 1; i < process_count; i++) {
/* Send local_size ints starting at array index (i * local_size) */
MPI_Send(array + (i * local_size), local_size, MPI_INT, i, 0,
MPI_COMM_WORLD);
}
} else {
MPI_Recv(local_array, local_size, MPI_INT, 0, 0, MPI_COMM_WORLD,
MPI_STATUS_IGNORE);
}In this code, the boss executes a loop that executes once for each worker
process, in which it sends the worker a piece of the array. It starts sending
data from the address of array at an offset of (i * local_size) to ensure
that each worker gets a unique piece of the array. That is, the worker with
rank 1 gets a piece of the array starting at index 5, rank 2 gets a piece of
the array starting at index 10, etc., as shown in Figure 2.
Each call to MPI_Send sends local_size (5) integers worth of data (20
bytes) to the process with rank i. The 0 argument toward the end represents
a message tag, which is an advanced feature that this program doesn’t need — setting it to 0 treats all messages equally.
The workers all call MPI_Recv to retrieve their piece of the array, which
they store in memory at the address to which local_array refers. They receive
local_size (5) integers worth of data (20 bytes) from the node with rank 0.
Note that MPI_Recv is a blocking call, which means that a process that
calls it will pause until it receives data. Because the MPI_Recv call
blocks, no worker will proceed until the boss sends its piece of the array.
Parallel Execution
After a worker has received its piece of the array, it can begin multiplying each array value by the scalar. Because each worker gets a unique subset of the array, they can execute independently, in parallel, without the need to communicate.
Aggregating Results
Finally, after workers complete their multiplication, they send the updated
array values back to the boss, which aggregates the results. Using
MPI_Send and MPI_Recv, this process looks similar to the array
distribution code above, except the roles of sender and receiver are reversed:
if (rank == 0) {
int i;
for (i = 1; i < process_count; i++) {
MPI_Recv(array + (i * local_size), local_size, MPI_INT, i, 0,
MPI_COMM_WORLD, MPI_STATUS_IGNORE);
}
} else {
MPI_Send(local_array, local_size, MPI_INT, 0, 0, MPI_COMM_WORLD);
}Recall that MPI_Recv blocks or pauses execution, so each call in the
for loop causes the boss to wait until it receives a piece of the array
from worker i.
Scatter/Gather
Although the for loops in the previous example correctly distribute data with MPI_Send and
MPI_Recv, they don’t succinctly capture the intent behind them. That is,
they appear to MPI as a series of send and receive calls without the obvious
goal of distributing an array across MPI processes. Because parallel
applications frequently need to distribute and collect data like this example
array, MPI provides functions for exactly this purpose: MPI_Scatter and
MPI_Gather.
These functions provide two major benefits:
-
They allow the entire code blocks above to each be expressed as a single MPI function call, which simplifies the code.
-
They express the intent of the operation to the underlying MPI implementation, which may be able to better optimize their performance.
To replace the first loop above, each process could call MPI_Scatter:
/* Boss scatters chunks of the array evenly among all the processes. */
MPI_Scatter(array, local_size, MPI_INT, local_array, local_size, MPI_INT,
0, MPI_COMM_WORLD);This function automatically distributes the contents of memory starting at
array in pieces containing local_size integers to the local_array
destination variable. The 0 argument specifies that the process with rank 0
(the boss) is the sender, so it reads and distributes the array source to
other processes (including sending one piece to itself). Every other process
acts as a receiver and receives data into its local_array destination.
After this single call, the workers can each multiply the array in parallel.
When they finish, each process calls MPI_Gather to aggregate the results
back in the boss’s array variable:
/* Boss gathers the chunks from all the processes and coalesces the
* results into a final array. */
MPI_Gather(local_array, local_size, MPI_INT, array, local_size, MPI_INT,
0, MPI_COMM_WORLD);This call behaves like the opposite of MPI_Scatter: this time, the 0
argument specifies that the process with rank 0 (the boss) is the receiver, so
it updates the array variable, and workers each send local_size integers
from their local_array variables.
Full Code for MPI Scalar Multiply
Here’s a full MPI scalar multiply code listing that uses MPI_Scatter and
MPI_Gather
(scalar_multiply_mpi.c):
#include <stdio.h>
#include <stdlib.h>
#include "mpi.h"
#define ARRAY_SIZE (40)
#define SCALAR (10)
/* In a real application, the boss process would likely read its input from a
* data file. This example program produces a simple array and informs the
* caller of the size of the array through the array_size pointer parameter.*/
int *build_array(int *array_size) {
int i;
int *result = malloc(ARRAY_SIZE * sizeof(int));
if (result == NULL) {
exit(1);
}
for (i = 0; i < ARRAY_SIZE; i++) {
result[i] = i;
}
*array_size = ARRAY_SIZE;
return result;
}
/* Print the elements of an array, given the array and its size. */
void print_array(int *array, int array_size) {
int i;
for (i = 0; i < array_size; i++) {
printf("%3d ", array[i]);
}
printf("\n\n");
}
/* Multiply each element of an array by a scalar value. */
void scalar_multiply(int *array, int array_size, int scalar) {
int i;
for (i = 0; i < array_size; i++) {
array[i] = array[i] * scalar;
}
}
int main(int argc, char **argv) {
int rank, process_count;
int array_size, local_size;
int scalar;
int *array, *local_array;
/* Initialize MPI */
MPI_Init(&argc, &argv);
/* Determine how many processes there are and which one this is. */
MPI_Comm_size(MPI_COMM_WORLD, &process_count);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
/* Designate rank 0 to be the boss. It sets up the problem by generating
* the initial input array and choosing the scalar to multiply it by. */
if (rank == 0) {
array = build_array(&array_size);
scalar = SCALAR;
printf("Initial array:\n");
print_array(array, array_size);
}
/* Boss sends the scalar value to every process with a broadcast.
* Worker processes receive the scalar value by making this MPI_Bcast
* call. */
MPI_Bcast(&scalar, 1, MPI_INT, 0, MPI_COMM_WORLD);
/* Boss sends the total array size to every process with a broadcast.
* Worker processes receive the size value by making this MPI_Bcast
* call. */
MPI_Bcast(&array_size, 1, MPI_INT, 0, MPI_COMM_WORLD);
/* Determine how many array elements each process will get.
* Assumes the array is evenly divisible by the number of processes. */
local_size = array_size / process_count;
/* Each process allocates space to store its portion of the array. */
local_array = malloc(local_size * sizeof(int));
if (local_array == NULL) {
exit(1);
}
/* Boss scatters chunks of the array evenly among all the processes. */
MPI_Scatter(array, local_size, MPI_INT, local_array, local_size, MPI_INT,
0, MPI_COMM_WORLD);
/* Every process (including boss) performs scalar multiplication over its
* chunk of the array in parallel. */
scalar_multiply(local_array, local_size, scalar);
/* Boss gathers the chunks from all the processes and coalesces the
* results into a final array. */
MPI_Gather(local_array, local_size, MPI_INT, array, local_size, MPI_INT,
0, MPI_COMM_WORLD);
/* Boss prints the final answer. */
if (rank == 0) {
printf("Final array:\n");
print_array(array, array_size);
}
/* Clean up. */
if (rank == 0) {
free(array);
}
free(local_array);
MPI_Finalize();
return 0;
}In the main function, the boss sets up the problem and creates an array.
If this were solving a real problem (for example, a scientific computing application),
the boss would likely read its initial data from an input file. After
initializing the array, the boss needs to send information about the size of
the array and the scalar to use for multiplication to all the other worker
processes, so it broadcasts those variables to every process.
Now that each process knows the size of the array and how many processes there are, they can each divide to determine how many elements of the array they’re responsible for multiplying. For simplicity, this code assumes that the array is evenly divisible by the number of processes.
The boss then uses the MPI_Scatter function to send an equal portion of the
array to each worker process (including itself). Now the workers have all the
information they need, so they each perform multiplication over their portion
of the array in parallel. Finally, as the workers complete their
multiplication, the boss collects each worker’s piece of the array using
MPI_Gather to report the final results.
Compiling and executing this program looks like this:
$ mpicc -o scalar_multiply_mpi scalar_multiply_mpi.c $ mpirun -np 8 --hostfile hosts.txt ./scalar_multiply_mpi Initial array: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 Final array: 0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 260 270 280 290 300 310 320 330 340 350 360 370 380 390
15.2.6. Distributed Systems Challenges
In general, coordinating the behavior of multiple processes in distributed systems is notoriously difficult. If a hardware component (e.g., CPU or power supply) fails in a shared memory system, the entire system becomes inoperable. In a distributed system though, autonomous nodes can fail independently. For example, an application must decide how to proceed if one node disappears and the others are still running. Similarly, the interconnection network could fail, making it appear to each process as if all the others failed.
Distributed systems also face challenges due to a lack of shared hardware, namely clocks. Due to unpredictable delays in network transmission, autonomous nodes cannot easily determine the order in which messages are sent. Solving these challenges (and many others) is beyond the scope of this book. Fortunately, distributed software designers have constructed several frameworks that ease the development of distributed applications. We characterize some of these frameworks in the next section.
MPI Resources
MPI is large and complex, and this section hardly scratches the surface. For more information about MPI, we suggest:
-
The Lawrence Livermore National Lab’s MPI tutorial, by Blaise Barney.
-
CSinParallel’s MPI Patterns.
